北京交通大学2024年工程博士专业学位申请考核制全日制定向就业类别考生考核项目参考书目及考试大纲
2024年一年一度的博士招生考试即将开始了,目前清华大学、浙江大学等院校已经公岸上了2024年博士招生简章。接下来我们将迎来2024年的博士招生序幕,华慧考博老师将及时为大家更新其他各院的招生简章信息!各位考生如有关于考博的其他问题,欢迎大家来华慧考博咨询。
一般情况下,2024年博士招生简章将会在2023年的九月份至2024年的3月左右集依次由各院校研究生院官网发布,有意在2024年参加博士招生考试的同学千万不要错过这段时间。也可多关注华慧考博网,第一时间了解全国各院校2024年考博招生信息!
如对考博备考有任何疑问,请大家关注华慧考博频道或者咨询华慧考博官方电话(QQ同步)4006224468,华慧考博2群:181131985、华慧考博6群:434135037、华慧考博7群:176325252、华慧考博4群:184307274.入群确认信息请填写(华慧考博咨询老师)加入群以后,请务必修改你的群名片为你的姓名。谢谢大家!
北京交通大学2024年工程博士专业学位申请考核制全日制定向就业类别考生考核项目参考书目及考试大纲
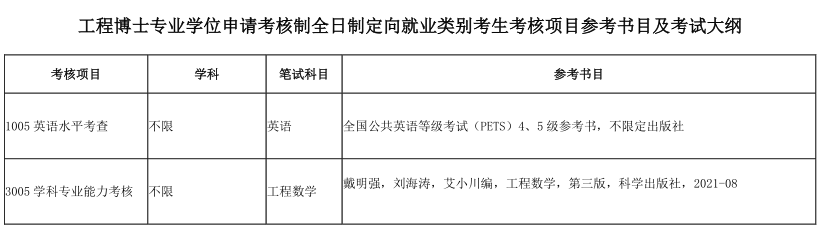
工程数学考试大纲:
一、行列式
考试内容:行列式的概念和基本性质行列式按行(列)展开定理考试要求:
1.了解行列式的概念,掌握行列式的性质.
2.会应用行列式的性质和行列式按行(列)展开计算行列式.
二、矩阵
考试内容:矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换矩阵等价
考试要求:
1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵和反对称矩阵以及它们的性质.
2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.
3.理解逆矩阵的概念,掌握逆矩阵的性质,以及矩阵可逆的充分必要条件,理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.
4.理解矩阵的初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.
三、向量
考试内容:向量的概念向量的线性组合和线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量空间n维向量空间的基变换和坐标变换过渡矩阵向量的内积线性无关向量组的正交规范化方法规范正交基正交矩阵及其性质
考试要求:
1.理解n维向量、向量的线性组合与线性表示的概念.
2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.
3.理解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.
4.理解向量组等价的概念,理解矩阵的秩与其行(列)向量组的秩之间的关系.
5.了解n维向量空间、子空间、基底、维数、坐标等概念.
6.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.
7.了解规范正交基、正交矩阵的概念以及它们的性质.
四、线性方程组
考试内容:线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件解空间考试要求
1.会用克莱姆法则.
2. 理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.
3.理解齐次线性方程组的基础解系、通解及解空间的概念,掌握齐次线性方程组的基础解系和通解的求法.
4.掌握用初等行变换求解线性方程组的方法.
五、矩阵的特征值及特征向量
考试内容:矩阵的特征值和特征向量的概念、性质相似变换、相似矩阵的概念及性质矩阵可相似对角化的充分必要条件实对称矩阵的特征值、特征向量
考试要求:
1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵的特征值和特征向量.
2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,掌握将矩阵化为相似对角矩阵的方法.
3.掌握实对称矩阵的特征值和特征向量的性质.
六、二次型
考试内容:二次型及其矩阵表示二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性
考试要求:
1.掌握二次型及其矩阵表示,了解二次型秩的概念,了解二次型的标准形、规范形的概念以及惯性定理.
2.掌握用正交变换化二次型为标准形的方法,会用配方法化二次型为标准形.
3.理解正定二次型、正定矩阵的概念,并掌握其判别法.
七、随机事件和概率
考试内容:随机事件与样本空间事件的关系与运算完备事件组概率的概念概率的基本性质条件概率基本公式事件的独立性独立重复试验
考试要求:
1.了解样本空间(基本事件空间)的概念,理解随机事件的概念,掌握事件的关系与运算.
2.掌握概率的加法公式、减法公式、乘法公式、全概率公式,以及贝叶斯(Bayes)公式.
3.理解事件独立性的概念,掌握用事件独立性进行概率计算;理解独立重复试验的概念.
八、随机变量及其分布
考试内容:随机变量随机变量的分布函数的概念及其性质离散型随机变量的概率分布连续型随机变量的概率密度常见随机变量的分布随机变量函数的分布
考试要求:
1.理解随机变量的概念.理解分布函数的概念及性质.会计算与随机变量相联系的事件的概率.
2.理解离散型随机变量及其概率分布的概念,掌握0-1分布、二项分布、泊松分布及其应用.
3.理解连续型随机变量及其概率密度的概念,掌握均匀分布、正态分布、指数分布及其应用
4.会求随机变量函数的分布.
九、多维随机变量及其分布
考试内容:多维随机变量及其分布二维离散型随机变量的概率分布、边缘分布和条件分布二维连续型随机变量的概率密度、边缘概率密度和条件密度随机变量的独立性和不相关性
考试要求:
1.理解多维随机变量的概念,理解多维随机变量的分布的概念和性质.理解二维离散型随机变量的概率分布、边缘分布和条件分布,理解二维连续型随机变量的概率密度、边缘密度和条件密度,会求与二维随机变量相关事件的概率.
2.理解随机变量的独立性及不相关性的概念,掌握随机变量相互独立的条件.
十、随机变量的数字特征
考试内容:随机变量的数学期望(均值)、方差、标准差及其性质随机变量函数的数学期望协方差、相关系数及其性质
考试要求:
1.理解随机变量数字特征(数学期望、方差、标准差、协方差、相关系数)的概念,会运用数字特征的基本性质,并掌握常用分布的数字特征.
2.会求随机变量函数的数学期望.
十一、数理统计的基本概念
考试内容:总体个体简单随机样本统计量样本均值样本方差和样本矩卡方分布T分布F分布分位数正态总体的常用抽样分布
考试要求:
1.理解总体、简单随机样本、统计量、样本均值、样本方差的概念
2.了解卡方分布、T分布和F分布的概念及性质.
十二、参数估计
考试内容:点估计的概念估计量与估计值最大似然估计法估计量的评选标准区间估计的概念单个正态总体的均值和方差的区间估计
考试要求:
1.理解参数的点估计、估计量与估计值的概念.
2.掌握最大似然估计法.
3.了解估计量的无偏性、有效性和一致性的概念,并会验证估计量的无偏性.
4.理解区间估计的概念,会求单个正态总体的均值和方差的置信区间.
相关阅读:北京交通大学2024年工程博士专业学位研究生招生简章
温馨提示:因考试政策、内容不断变化与调整,本网站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!









